我们究竟如何模拟股票价格的走势?(一)
在上一篇文章:Deep Hedging - 使用深度学习找到的最佳对冲策略 中,我们提到为了验证一个对冲算法的风险属性,需要对某一股票(标的资产)的价格走势进行大量的计算机模拟,得到在\(10^6\)种不同情况下期权合同的最终收益,然后分析这些最终收益的统计学特征(比如第一个百分位数),以此作为期权定价的基准。我们模拟的每一条股价走势,都代表了一组随机变量的某种特定取值,以及市场在这种随机情况下的表现。我们一般不会单纯使用历史数据来预测未来股价的走势,因为总会有一些 “史无前例”的情况发生,并且这些情况通常带来巨大的影响,却是我们要格外小心的。
所以,在实际操作中,我们首先为随机模型(Stochastic Model)确定参数的取值,这个过程叫做“模型参数率定” (Model Calibration)。然后,我们将参数带入模型的表达式,并根据它的性质采用合适的方法模拟未来股票价格的走势,将上百万次的模拟当作未来可能发生的各种情况,分析我们的对冲(或投资)算法在这些情况中的综合表现,来确定这个算法是不是满足设计要求。
本文中,我们会介绍几个在模拟金融时间序列(比如股票价格,汇率价格)时,最经典的随机模型。
布朗运动:历史渊源
如今,布朗运动(Brownian Motion)并不直接用于金融产品价格的模拟,但是它几乎一切模型的基础。
1827年,苏格兰植物学家罗伯·特布朗(Robert Brown)首次在显微镜下观察到悬浮花粉在水中的无规则运动。在将近八十年之后,阿尔伯特·爱因斯坦(Albert Einstein)于1905年在德语期刊 Annalen der Physik(译:物理学年鉴)上发表了一篇文章,他提出了花粉的运动是由于水分子的推动,从而验证了水分子的存在和分子热运动的特性,并且他还首次提出了这一现象的数学推导。从此,人类获得了一套可以模拟自然界中随机现象的方法和理论。这实际上是爱因斯坦的第一个主要科学成就,1905年后来被称作爱因斯坦的 “奇迹年”。

然而,关于金融资产价格随机性理念的出现,其实是在爱因斯坦之前。1900年,一位法国的数学家Louis Bachelier提交了一篇题目为 Théorie de la speculation(译:投机理论)的博士毕业论文。他在论文中提出如果金融产品的价格中存在某些规律,并且这些规律可以被预测。那么投机者就会发现并利用它们,于是它们也就不存在了。可惜的是,在那个几乎没有人会把数学和一个叫做“金融”的学科联系起来的年代,Bachlier的想法实在是过于先进了,以至于他的论文被人们忽略了超过六十年。一直到上个世纪六十年代,美国经济学家保罗·萨缪尔森(Paul Samuelson)发现了Bachlier的论文,受到很大的启发。1965年,保罗在Bachlier想法的基础上发表了一篇题为 Proof That Properly Anticipated Prices Fluctuate Randomly(译:证明可预见价格之随机性)的论文,并且首次从数学角度说明了如果一个市场上的一切信息都是可以自由流动的,那么当前的市场价就已经包含了所有能被预测的因素。于是,其他所有可以引起价格变化的机制,就只能是随机因素。这一理论后来被称作有效市场假说(Efficient Market Hypothesis)。
从此,人们开始使用随机模型来模拟金融资产的价格曲线。
布朗运动:随机游走和维纳过程
英国统计学家弗朗西斯·高尔顿(Francis Galton)爵士发明了高尔顿板(Galton Board)用来演示中心极限定理(Central Limit Theory)。
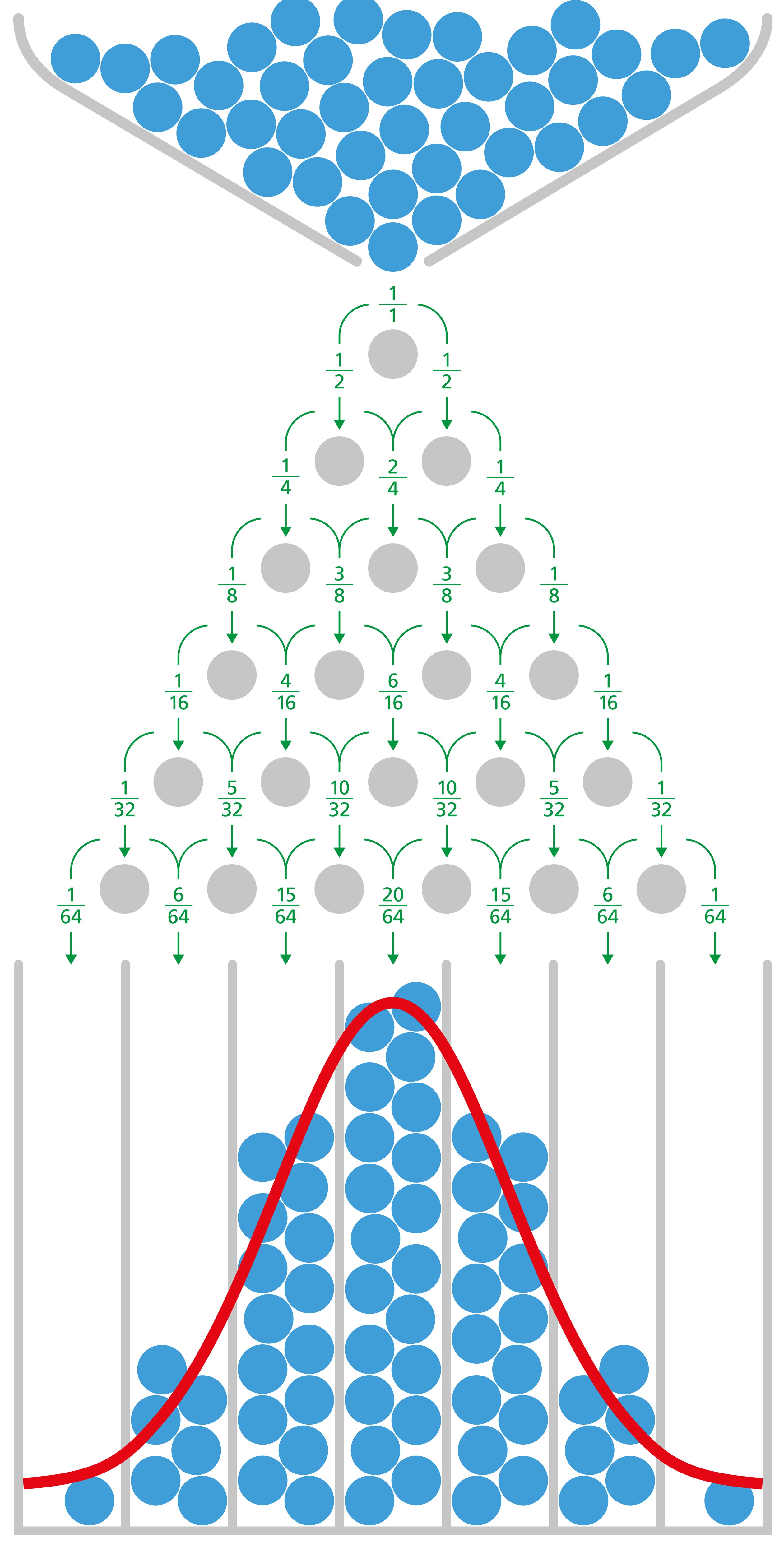
图中的每一个蓝色小球需要走六步才能到达下面的网格。这其中,每一步只有两个选择,向左或者向右,并且概率都是50%。我们可以看到,大多数的小球落在了最中间的那一栏,落在最左边一栏和最右边一栏的小球是最少的。这个演示可以被看作是一种随机游走(Random Walk)过程,这个过程一共六步。每一步的选择相互独立,但又是完全相同的可能性和概率。使用中心极限定理,我们知道所有小球最终的位置应该符合正态分布。
如果我们把这张图片逆时针旋转90度,并且想象成一个物体从坐标轴(0,0)的位置出发,向右移动。对于它的每一步,同样是独立又完全相同的可能性和概率。如果它每一步在X轴上移动的距离无限小,我们就会得到一条类似于下图中的路径:
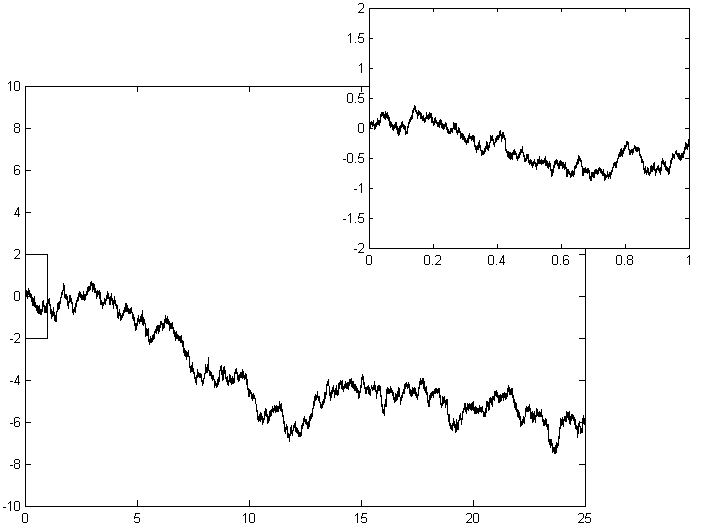
这就是维纳过程(Wiener process)。它其实就是每一步距离无限小随机游走过程。有的人也把它叫做布朗运动。这就是罗伯特·布朗观察到花粉随机运动的一种数学解释。
存在趋势的布朗运动
从数学的角度,存在趋势的布朗运动 \(S(t)\) 需要满足以下这个随机微分方程(stochastic differential equation):
\(dS(t)=\mu dt+\sigma dW(t)\),初始值为: \(S(0)=s_0\)
直接对它求积分,可得:
\(S(t) = s_0 + \mu t + \sigma W(t)\)
这里的 \(W(t)\) 代表一个上文提到的维纳过程。
\(s_0\) 代表这个股票的初始价格。我们可以随意的取值,或者采用市场上的真实价格。比如中国石化(600028)在2021年5月21日的收盘价是4.36元,然后我们定义 \(S(1)\) 代表什么,如果它是中国石化在2021年5月24日的收盘价,那么 \(t\) 就代表的是交易日的序列。当然它也可以代表月份,小时,分钟或者任何的时间范围。
\(S(t)\) 代表这只股票在 \(t\) 时刻的价格,它是由一个常数 \(s_0\) ,一个时间的线性函数 \(\mu t\) ,和一个缩放的维纳过程 \(\sigma W(t)\) 相加而成。我们习惯把 \(\mu\) 当作这个股票价格变化的长期趋势,通常参考市场上无风险利率的取值。\(\sigma \) 其实代表了股价的波动率,因为它决定了随机因素对股价的影响。
到此为止,我们得到了一个可以模拟股票价格走势的方法。比如我们需要模拟未来10个交易日的股价:
- 首先生成10个相互独立的标准正态分布随机数。
- 计算维纳过程\(W(t)\)在t = 1,2,3 …… 10时的取值。
- 确定相关变量\(s_0\), \(\mu\) 和 \(\sigma\)的取值。
- 使用维纳过程和这些变量,计算股票在10个日期的价格\(S(1)\), \(S(2)\), \(S(3)\) …… \(S(10)\)。
当然,我们不能只有一条可能的价格走势,我们需要模拟大量不同的维纳过程以代表不同的随机情况,然后得到相应的股票价格曲线。
几何布朗运动
或许已经有人注意到,以上提出的方法有一个致命的缺陷。当 \(\sigma\) 的取值很大,同时 \(\mu\) 的值很小的时候,股票价格 \(S(t)\) 有可能会成为负数,这是绝对不符合现实情况的。所以,我们使用几何布朗运动(Geometric Brownian Motion)模型解决这个问题,它的随机微分方程为:
\(dS(t) = \mu S(t)dt + \sigma S(t) dW(t)\),初始值为: \(S(0)=s_0\)
我们可以得到:
\(S(t) = S(0) exp[(\mu - \frac{\sigma^{2}}{2})t+\sigma W(t)]\)
这个模型实际上是把股票价格的收益率 \(\frac{S(t)}{S(0)}\) 当作了一个布朗运动的指数函数,这似乎更符合金融实践中的习惯。并且股票价格 \(S(t)\) 也无法再成为一个负数。
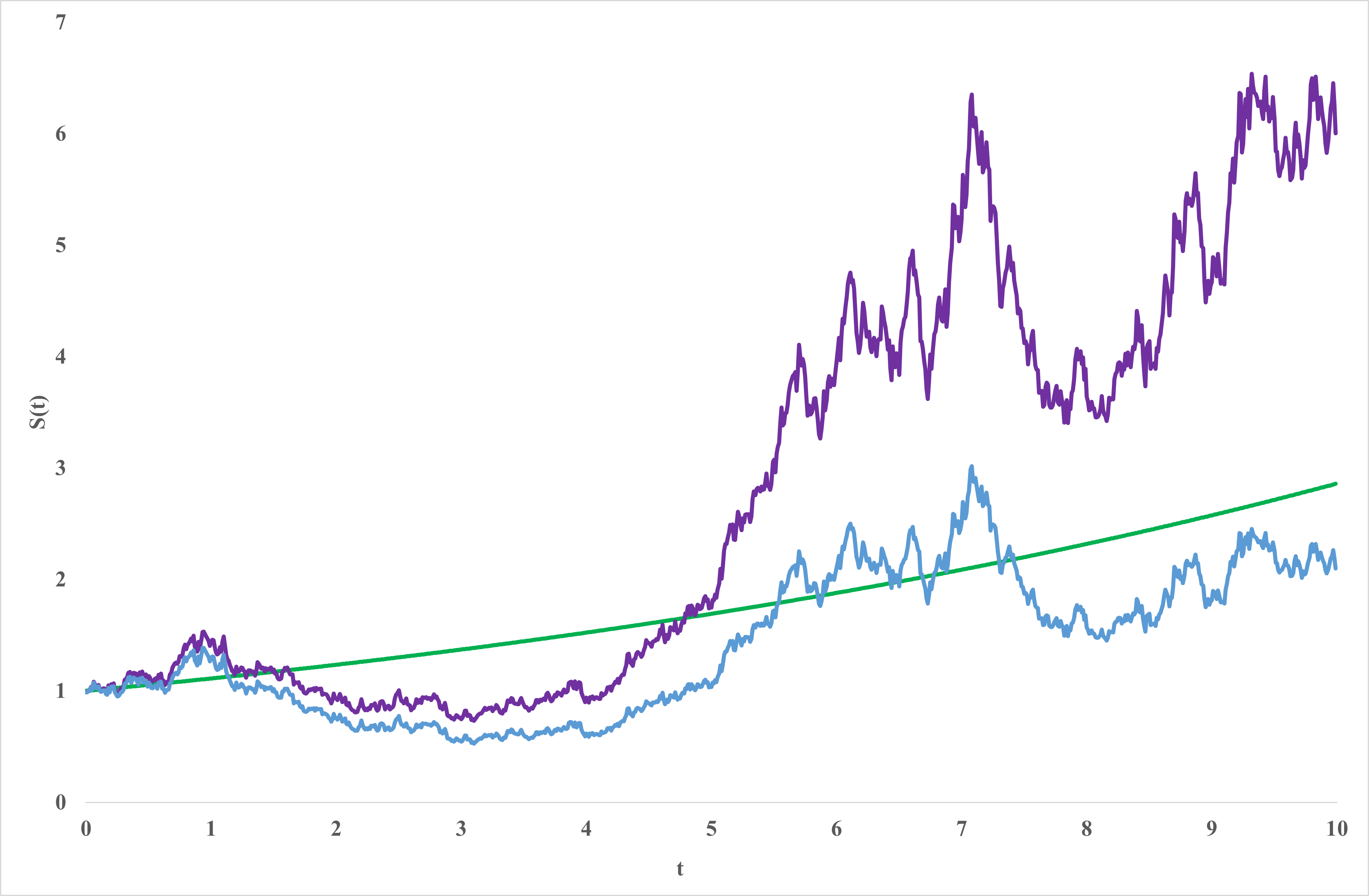
这个图中有三条线。其中紫色曲线是模拟的股票价格曲线 \(S(t)\) 。绿色的曲线代表他的线性因素 \(exp[(\mu - \frac{\sigma^{2}}{2})t]\) ,蓝色曲线是他的随机因素 \(exp[\sigma*W(t)]\) 。生成图中曲线的参数取值为:\(S_0 = 1\),\(\mu = 0.15\) 和 \(\sigma = 0.3\)。
对于几何布朗运动,\(\sigma\)的取值并不因为\(t\)的变化而有任何的改变。这意味着,股价的波动率是恒定的。我们从现实观察中可以得知,股价的波动并不是这样。在某些特殊时刻(比如重大政治经济事件发生时),股票市场会有明显更加剧烈的波动。所以,不光是股票价格\(S(t)\),我们也需要把随机因素引入股价波动率\(\sigma\)的模型之中,这就是随机波动模型(stochastic volatility models)。
(未完待续)
参考资料:
Einstein, Albert. "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen." Annalen der physik 4 (1905).
Bachelier, Louis. "Théorie de la spéculation." In Annales scientifiques de l'École normale supérieure, vol. 17, pp. 21-86. 1900.
Samuelson, Paul A. "Proof That Properly Anticipated Prices Fluctuate Randomly." Management Review 6, no. 2 (1965).
https://en.wikipedia.org/wiki/Brownian_motion
https://en.wikipedia.org/wiki/Wiener_process
https://www.cantorsparadise.com/brownian-motion-in-financial-markets-ea5f02204b14
http://www.mi.uni-koeln.de/wp-znikolic/wp-content/uploads/2017/05/4_Geometric_Brownian_Motion_28042017.pdf
点击数:1977
