Deep Hedging --- 使用深度学习找到的最佳对冲策略
使用神经网络为金融衍生品定价(Pricing)和设计对冲(Hedging)策略,最早可以追溯到1994年。基于神经网络模型的通用近似性质(Universal Approximation Property), Hutchinson首次提出可以将它们作为传统偏微分方程定价方法的补充,并且使用了1987至1991年标普500期货的数据进行了实验。
自Hutchinson之后,这个方向的研究却没有太多发展,主要还是由于神经网络模型的训练需要强大的计算能力。直至最近的5-10年,这样的条件才能在业界和学术界得到广泛地满足。

Deep Hedging模型出现在2018年。论文的作者来自摩根大通(JP Morgan)和苏黎世联邦理工学院(ETH),所以我们相信这种基于神经网络的期权定价和对冲模型已经或多或少地运用在了实际的交易当中。
背景假设
假设你是一个看涨期权(Call Option)的发行人(Issuer),并且这个期权是欧式期权(European Option)。意味着期权的买方只能在期权的到期日行使期权,我们假设是30天之后。在这30天的过程中,你需要不断地买入或者卖出期权的标的资产(Underlying Asset)以对冲你暴露在这个交易中的风险。在理想状况下,如果没有交易成本,并且可以连续交易(每一秒钟不断地平衡仓位),那么30天之后,你可以保证没有任何盈利或者损失。但是现实中这两点都实现不了,所以在期权到期时,你会产生一笔损失,而期权的初始价格(期权合同开始时对方支付给你的用于购买期权的钱)就应当基于你对于这笔损失的预期。
经典理论的不足
在经典的Black-Scholes-Merton模型中,期权的初始价格和每一次对冲仓位所需要买入或者卖出的标的资产数量,都可以通过方程计算出来。但是这套理论基于以下三个不切实际的假设:1. 没有交易成本;2. 可以无限连续交易;3. 标的资产的价格变化符合几何布朗运动(Geometric Brownian Motion),即每一次价格的变化比例符合对数正态分布(Lognormal Distribution),并且其方差是个恒定的常数。前两点假设显然过于不切实际,第三点也可以被很多现实中的观测结果推翻。比如肥尾效应(Fat Tail)和波动率微笑现象(Volatility Smile)。很多理论认为,2008年的国际金融危机的起因之一就是人们对于肥尾效应的估计不足。
我们有许多比GBM更加符合实际的金融时间序列模型,Heston模型就是其中之一。在Heston中,资产的价格和他的方差中各有一个随机因子。方程式如下:
\[dS(t, S) = \mu S dt + \sqrt{v} S dW_1\]
\[dv(t, S) = \kappa (\theta - v) dt + \sigma \sqrt{v} dW_2\]
\[dW_1 dW_2 = \rho dt\]
\(W_1\) 和 \(W_2\) 各为一个标准正太分布的随机变量,他们之间的关联系数(Correlation)为 \(\rho\)。 \(S\) 代表资产的价格,\(v\) 代表他的方差。其他都是常数。
如果标的资产的价格符合Heston模型,那么经典的Black-Scholes-Merton方法就已经得不到合理的期权价格和对冲策略。更别说考虑交易成本和交易频率的问题。
Deep Hedging正是从这个角度入手,在第一条和第三条理想化假设都不满足的情况下,使用神经网络模型找到对冲策略,根据不同的风险偏好(Risk Appetite)或者不同的效用函数(Utility Function)优化神经网络中的参数。至于第二条假设,Deep Hedging只是默认规律地每天进行一次对冲交易。
神经网络结构
Deep Hedging模型的神经网络部分并不复杂,甚至相对一些著名的用于图像识别的神经网络,都不能算是深(Deep)。网络只有两层,都是全连接层(Fully Connected Layer),各有15个神经元。再加上一个输入层,一个输出层,共四层。如下图:
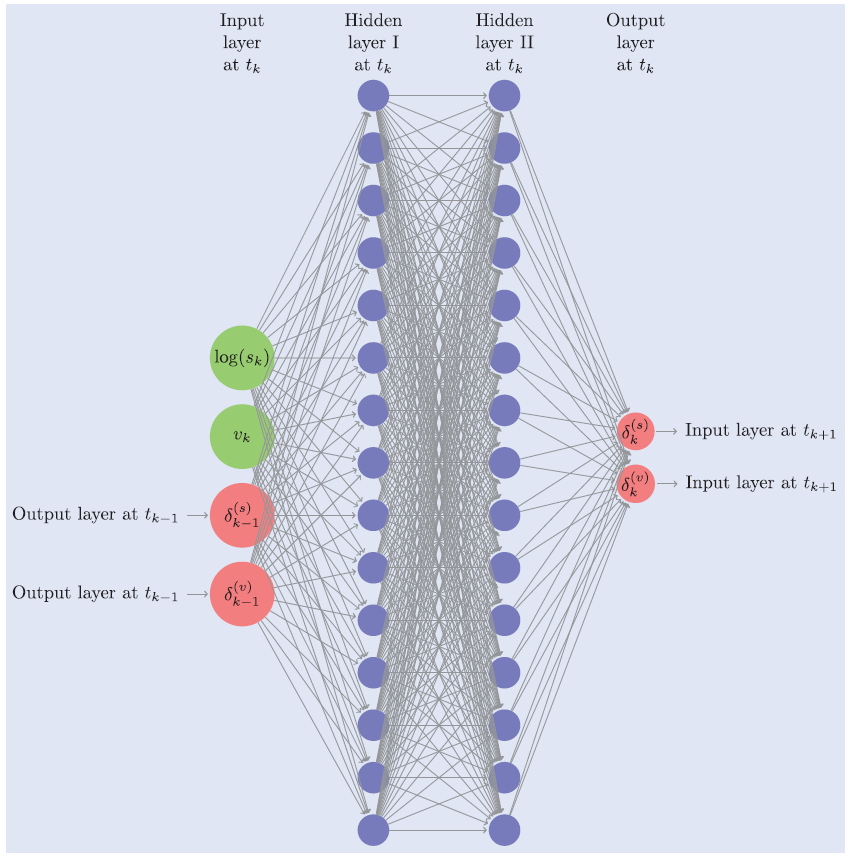
图源:Deep Hedging 论文
独特的损失函数
除此之外,由于神经网络可以使用不同的损失函数(Loss Function)对模型进行优化。在金融衍生品定价中,其实际上是代表了不同投资者的风险偏好,或者是他们的效用函数(即合同到期后产生的损失或收益,对投资人总体经济效用的影响)。所以Deep Hedging的损失函数和其他常见的深度学习模型(例如图像识别,或语音处理模型)非常不同。论文作者提出了两个可选的损失函数。一个是熵风险衡量(Entropy Risk Measure),方程如下:
\[\rho (X) := \frac{1}{\lambda}\log {E(e^{-\lambda X})}\]
\(\lambda\) 为大于零的常数,可以代表投资人的风险偏好。即 \(\lambda\) 越大,投资人可以接受的风险越大。模型的设计者可以自己选择 \(\lambda\) 的值,从而满足不同金融机构或者投资人的风险习惯,股东或者监管的投资限制和要求。
作者提出的另一个损失函数,就是基于监管文件中常见的预期损失(Expected Shortfall):
\[\rho(X) := \frac{1}{1-\alpha}\int_{0}^{1-\alpha}VaR_{\gamma}(X)d\gamma\]
这个方法的逻辑并不复杂。首先假设一个通常情况发生的概率,比如90%。然后计算所有剩余10%的极端情况发生后,发生损失的数学期望,然后将这个数学期望设定为对于风险的判定。所以,如果 \(\alpha\) 的值为99%,就比90%更加极端,那么计算出的预期损失就更大。在实际运用中,我们可以模拟106 条标的资产的价格走势,代表106 种可能的市场行情。然后运用对冲模型计算每一个情况下,当合同到期时的最终收益。然后计算其中1%最差的情况的平均损失,作为期权定价的基准。这里的 \(VaR\) 指的是风险价值(Value at Risk)。
通过使用直接与风险偏好关联的损失函数,Deep Hedging显然更符合金融衍生品市场参与者的习惯做法,并且更容易与监管要求相匹配。
总结
Deep Hedging开创了一个全新的领域:使用神经网络模型找寻标的资产价格和衍生品价格之间的非线性关系。这样的方法免去了许多传统BSM模型假设的限制,可以更加贴近现实中的场景。并且,将风险偏好融入损失函数之中使模型的可用性,以及可解释性大大增加。
但是,目前公布的Deep Hedging依然有许多提升的空间,比如交易频率不应该是规律性的以交易日为单位,而是根据标的价格的变化适时地对冲交易。神经网络的结构也过于简单,使用循环神经网络(Recurrent Neural Network)是明显更合适的选项。如果能将对于未来标的资产价格的预测,和对冲策略的训练相结合,将会是非常大的突破。
参考资料:
J. M. Hutchinson, A. W. Lo, and T. Poggio. A non-parametric approach to pricing and hedging deriva-tive securities via learning networks. The Journal of Finance, 49(3):851–889, 1994.
H. Buehler, L. Gonon, J. Teichmann, and B. Wood. Deep hedging. Quantitative Finance, 19(8):1271–1291, 2019.
注:论文中,作者其实是使用了标的资产和一个方差掉期(Variance Swap)的投资组合来对冲期权合同的风险。由于方差掉期过于复杂,本文没有提及。理论上单纯使用标的资产进行对冲也是可行的。
点击数:2916

